ROC(receiver operating characteristic)曲线通常被译为受试者工作特征曲线[1-2],美国生物统计百科全书[3]将其定义为“一种量化实验者、诊断者或预测者及其所用工具对存在混淆的两种状况或两种自然状态做出鉴别的准确程度的方法”,国内相关专业书籍[1-2]依据其曲线绘制方式将其定义为:“对诊断指标或模型预测概率的各个截断值,以1-特异度(假阳性率)为横坐标、以灵敏度(真阳性率)为纵坐标绘制的曲线即ROC曲线”。
ROC曲线分析起源于20世纪中期概率论和统计决策理论[4],最初用于描述雷达接收器对雷达信号与相关噪声的鉴别性能[5],故Receiver原意指雷达接收器,而Operating Characteristic这一术语源于质量控制领域,通常用于描述根据不同批次样品来区分产品质量优劣的可操作性特征[6]。1960年Lusted LB将ROC曲线分析应用于医学决策领域[7-9],1982年Swets等[10]总结了ROC曲线分析相关理论及其在生物医学方面的应用,此后ROC曲线分析广泛应用于筛检和诊断试验的评价,以及Logistic回归等预测模型的预测效果评价[11]。
ROC曲线应用领域虽广[12-15],但其主要用途可概括为以下三个方面:(1)描述基于定量指标(主要包括但不限于各类检测指标、仪器测试值、模型预测概率等定量指标)对二分类结局指标(如是否患病)做出预测的准确程度;(2)寻找定量指标用于预测结局指标的最佳截断值;(3)比较不同定量指标对同一结局指标的预测效能。ROC曲线综合考虑了灵敏度(sensitivity)和特异度(specificity),且与结局事件发生率无直接关系[11],通常被视为预测效果评价的最优方法[12,16-17]。但值得注意的是,ROC曲线与原始数据对应关系不够直观、主要借助统计软件绘制,其曲线下面积(area under curve,AUC)虽有理论释义,但在医学教育和实践中难以真切呈现[18],对于初学者和非专业人士而言通常较难理解。鉴于此,有必要探索针对ROC曲线及AUC的简单易解、形象直观的阐释方法,以加强使用者对这一重要工具的理解和应用。
一、ROC曲线含义
绘制ROC曲线及估计AUC的方法包括参数法和非参数法,当样本量较大时两种方法计算的AUC近似相等[17]。在实践中基于样本数据准确估计总体分布通常较为困难,故参数法的应用受到一定限制[14]。非参数法是常用统计软件计算AUC的主要方法,但也有的软件兼具两种方法。本文讨论范畴仅限非参数法。
非参数法即依据试验数据直接绘制ROC曲线,所绘制的曲线通常呈阶梯型。假定某试验拟评价某定量指标对某疾病的诊断效能,纳入经金标准诊断的病例数为na (number of abnormals)、非病例数为nn (number of normals),病例组定量指标平均检测值高于非病例组,在实际分析时若检测值高于截断值(cutoff value)则判定为阳性,反之判定为阴性。若na个病例和nn个非病例的检测值互不相同,则ROC曲线应包含na+nn+1个截断值(将na+nn个检测值排序后,介于其之间的截断值应有na+nn-1个,另有高于最高检测值和低于最低检测值的截断值各1个),将这些截断值所对应的坐标点(x=1-特异度,y=灵敏度)用线段连接起来就得到了ROC曲线。由最高截断值过渡至最低截断值对应ROC曲线由坐标点(0,0)过渡到坐标点(1,1),高于最高检测值的截断值对应(0,0)坐标点,低于最低检测值的截断值对应(1,1)坐标点。表1是某Logistic模型用于预测妊娠期高血压的示例数据,病例组和非病例组各10例。图1A给出了基于该示例数据[第(3)列和第(4)列]绘制的ROC曲线。
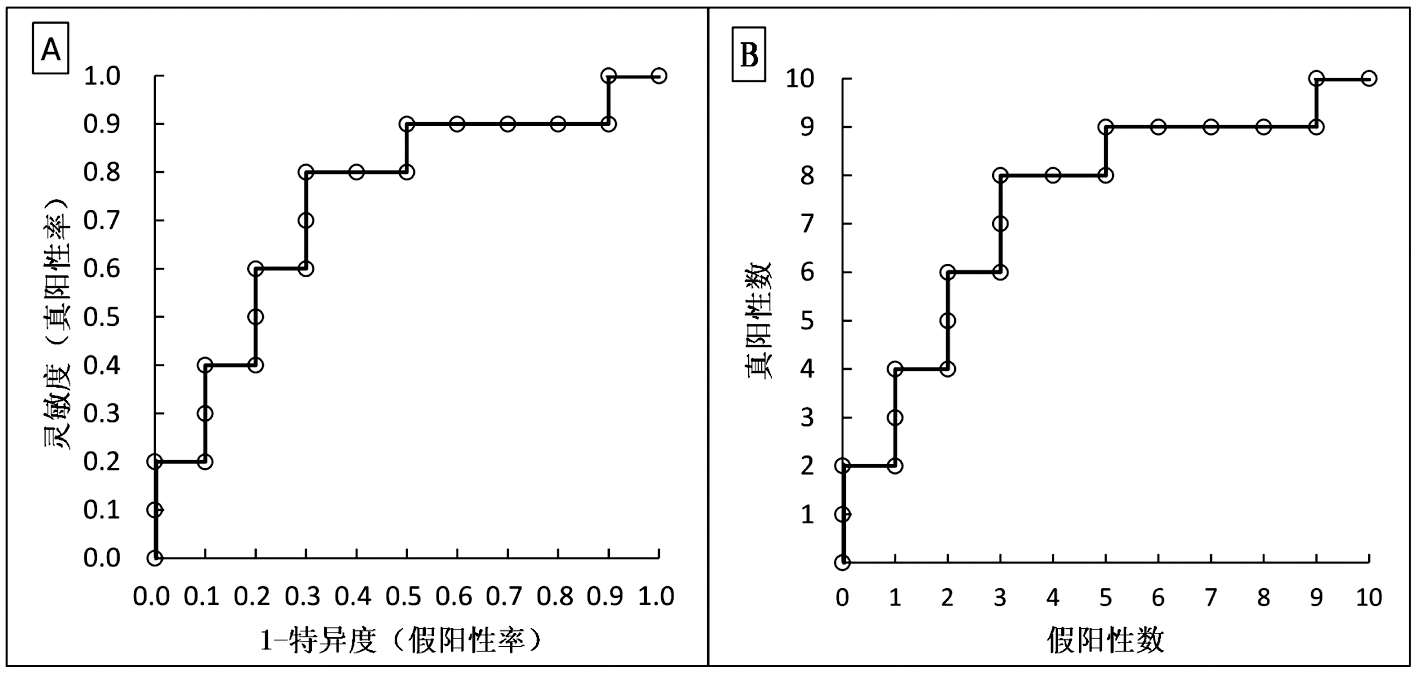
图A基于表1的第(3)、(4)列绘制,图B基于表1的第(5)、(6)列绘制
图1 ROC曲线(A)与非标化ROC曲线(B)
表1 某Logistic模型预测妊娠期高血压的示例数据
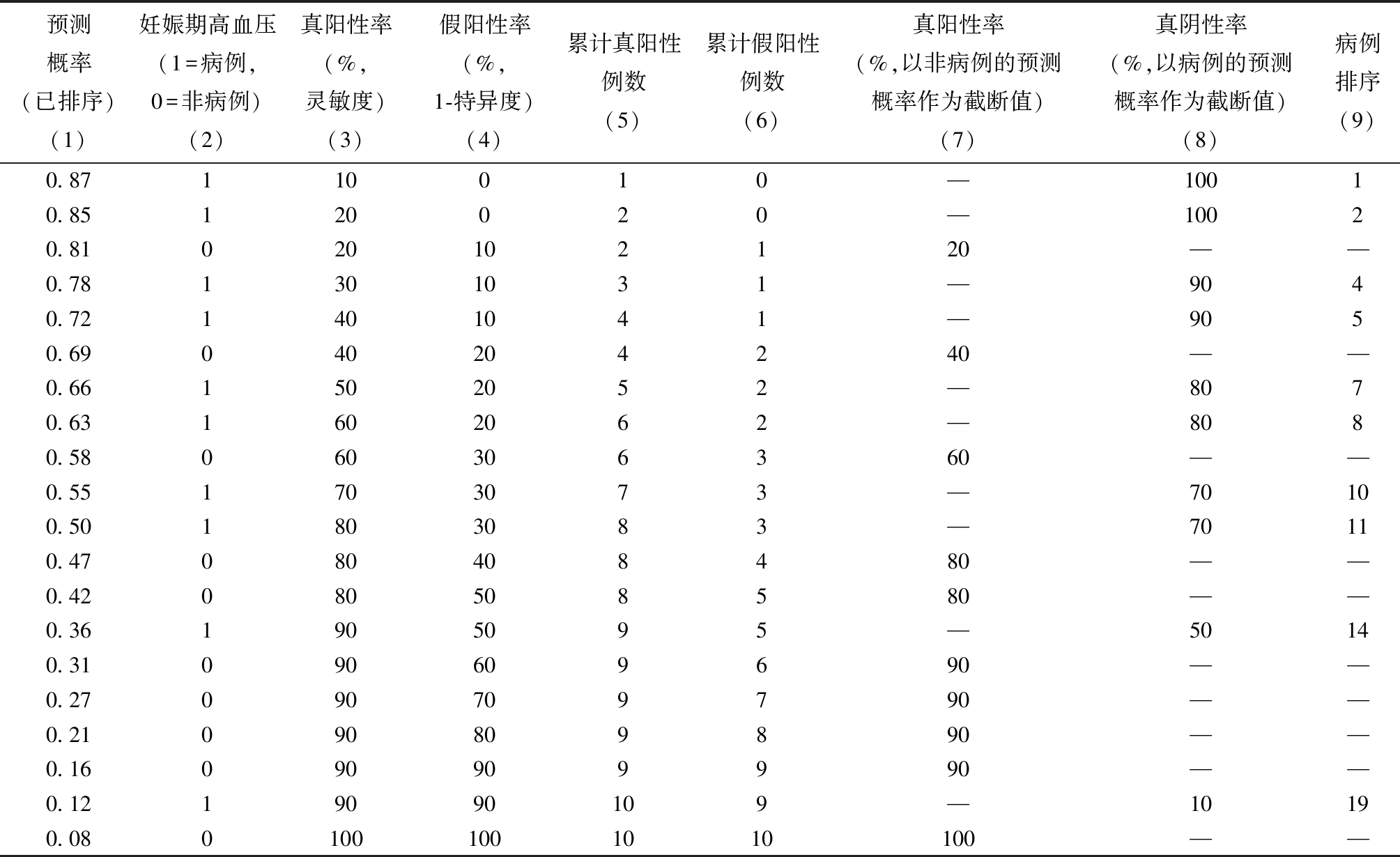
预测概率(已排序)(1)妊娠期高血压(1=病例,0=非病例)(2)真阳性率(%,灵敏度)(3)假阳性率(%,1-特异度)(4)累计真阳性例数(5)累计假阳性例数(6)真阳性率(%,以非病例的预测概率作为截断值)(7)真阴性率(%,以病例的预测概率作为截断值)(8)病例排序(9)0.87110010—10010.85120020—10020.81020102120——0.781301031—9040.721401041—9050.69040204240——0.661502052—8070.631602062—8080.58060306360——0.551703073—70100.501803083—70110.47080408480——0.42080508580——0.361905095—50140.31090609690——0.27090709790——0.21090809890——0.16090909990——0.1219090109—10190.0801001001010100——
为更好阐释ROC曲线含义,特此引入一个概念——非标化ROC曲线(unstandardized ROC curve)。非标化ROC曲线以真阳性数为纵坐标、假阳性数为横坐标,其绘制过程如下:(1)以高于最高检测值的截断值所对应的(0,0)坐标点为始点;(2)截断值由高到低每“挪动”一次,则诊断为阳性的对象数增加1例,若该对象确为病例,则真阳性数增加1例,假阳性数不变,反映在图形上为一条竖线;若该对象为非病例,则假阳性数增加1例,真阳性数不变,反映在图形上为一条横线;(3)曲线由左下向右上延伸直至低于最低检测值的截断值所对应的(nn,na)坐标点。图1B给出了基于表1示例数据[第(5)列和第(6)列]绘制的非标化ROC曲线。
非标化ROC曲线每条线段对应一个研究对象,竖线相当于病例,横线相当于非病例,故曲线形状取决于病例和非病例的检测值(或模型预测概率)排序。换言之,非标化ROC曲线相当于把病例和非病例按照检测值由高到低排列后的一维序次反映在了二维平面上。图2A更直观地展示了一维次序与二维非标化ROC曲线对应关系,图中一维次序红色实心圆表示病例,蓝色实心圆表示非病例,二维非标化ROC曲线红色竖线表示病例,蓝色横线表示非病例。理论上讲,当检测方法足够精确时,很难出现相同检测值[19]。但在实践中,若某个病例的检测值与某个非病例的检测值相等,则非标化ROC曲线会相应减少一个阶梯而多出一个斜坡。比如,若表1第11行第8个病例的模型预测概率由0.50变为0.47(与第12行第4个非病例的检测值相同),非标化ROC曲线则在相应位置出现一个斜坡(图2B紫色线段)。
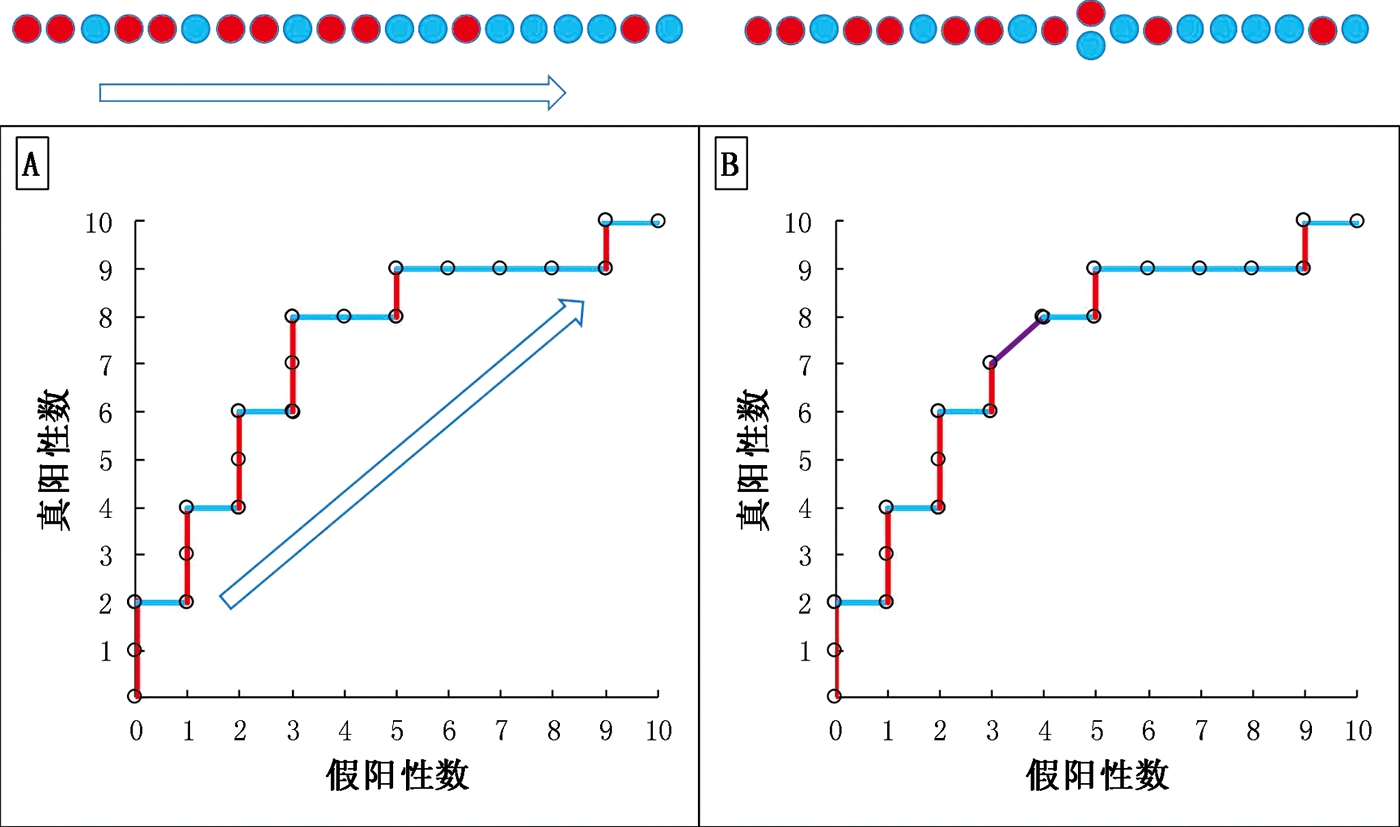
红色实心圆代指病例,蓝色实心圆代指非病例;红色竖线代指病例,蓝色横线代指非病例。图A中箭头所指为检测值(模型预测概率)由高到低的方向,可见一维的排序和粗ROC曲线的线段是一一对应的关系;图B所示为病例和非病例存在相同检查值(模型预测概率)时,在粗ROC曲线上体现为一斜线(紫色线段)
图2 一维次序与二维非标化ROC曲线对应关系
通过图1A和图1B对比可知,对于同样的试验数据,非标化ROC曲线与传统ROC曲线形状一致。传统ROC曲线可以理解为横纵坐标量纲标化后的非标化ROC曲线,即将非标化ROC曲线纵轴以病例总数为参比值做标化,标化后的纵轴即为真阳性率,将非标化ROC曲线横轴以非病例总数为参比值做标化,标化后的横轴即为假阳性率(即1 - 特异度)。
二、AUC含义与计算
AUC是ROC曲线分析最为重要的量化评价指标。通常认为,AUC介于0.5~0.7之间诊断价值较低,介于0.7~0.9之间诊断价值中等,大于0.9诊断价值较高[20]。非参数法AUC计算公式如下(与两个独立样本秩和检验统计量计算公式一致[21-22]):
(1)
其中,
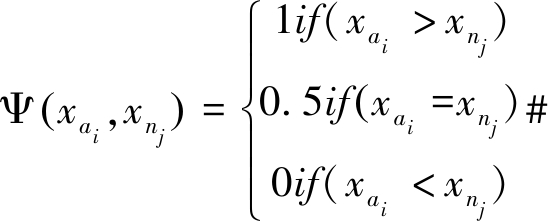
na和nn分别为病例数和非病例数,xai和xnj分别表示每个病例与非病例所对应的定量指标的检测值。公式含义如下:将na个病例所对应的检测值与nn个非病例所对应的检测值两两对比(共有na×nn组对比),在每一次比较中,若前者大于后者则Ψ=1,若前者小于后者则Ψ=0,若二者相等则Ψ=0.5,所有na×nn个Ψ的算术平均值即为AUC[12,16]。鉴于此,AUC可通俗理解为病例组每个检测值大于非病例组每个检测值的平均概率,或理解为随机选择的病例比随机选择的非病例更有可能被判定为病例的概率[22-23]。
基于非标化ROC曲线阐释AUC计算公式的含义更为直观。图3在图1B非标化ROC曲线的基础上增加了网格背景,同时将竖线所表示的病例标记为1、将横线所表示的非病例标记为0。如图所示,每条竖线将所有的0分为左右两部分,每条横线将所有的1分为上下两部分,图中绿色背景标识的格子数相当于非标化ROC曲线下面积。该面积可以看作每一行的曲线下面积之和,而每一行曲线下面积即为该行绿色格子数,取决于该行1的右侧有几个0,即取决于检测值比该病例更小的非病例的个数,所以xai>xnj时Ψ取1;当某个病例与某个非病例的检测值相同时,曲线线段为格子对角线,相对应的曲线下面积为0.5个格子,所以xai=xnj时Ψ取0.5;每行白色格子数取决于1的左侧有几个0,即取决于检测值比该病例更大的非病例的个数,因白色格子不计入AUC,所以xai<xnj时Ψ取0。前述AUC计算公式(1)的分子相当于绿色背景标识格子数,分母na×nn相当于总格子数,绿色背景标识格子数除以总格子数,相当于将带量纲的非标化ROC曲线下面积去量纲化,其大小等于AUC。
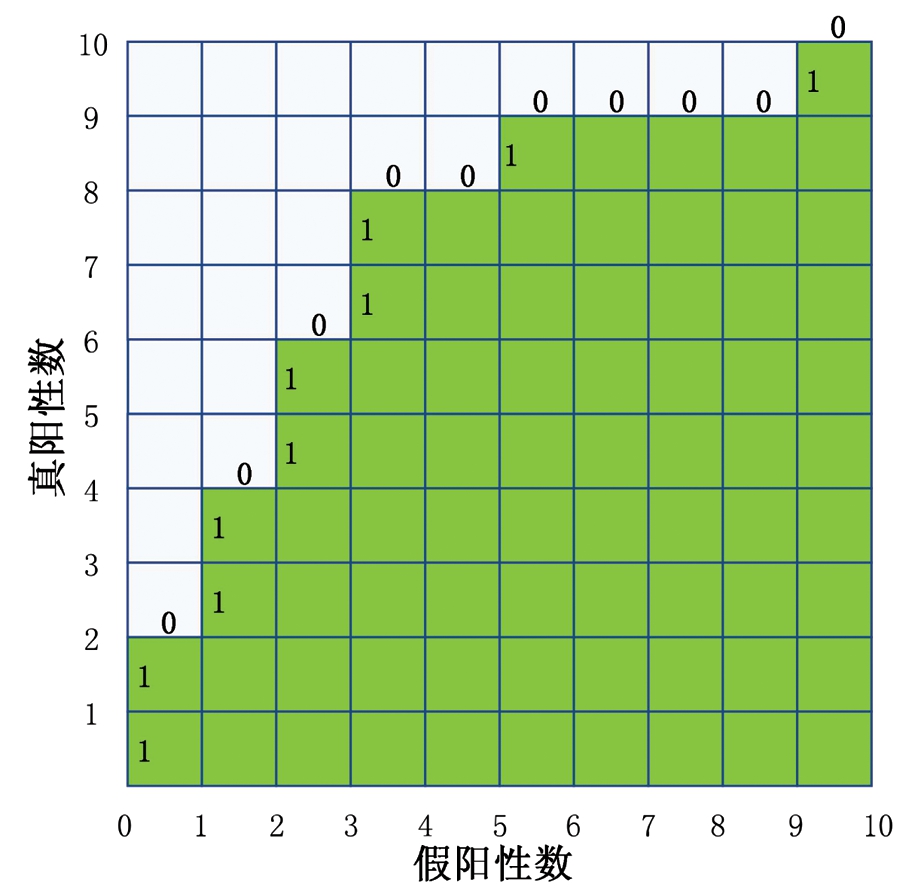
图3 设有背景网格的非标化ROC曲线
三、AUC含义延伸解读
公式(1)经简单变换可得到公式(2)和公式(3),公式(2)方括号内部为某一病例与所有非病例的比较结果,公式(3)方括号内部为某一非病例与所有病例的比较结果,两个公式方括号外部为对所有病例[公式(2)]或所有非病例[公式(3)]求算术平均值的过程。

(2)
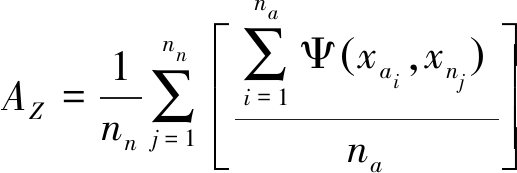
(3)
基于非标化ROC曲线,公式(2)方括号内部分可理解为某一行绿色格子数与该行总格子数nn(即非病例数)的比值,该比值反映该病例在所有非病例中的相对位置,即该病例检测值比非病例检测值更大的概率,方括号外的部分可理解为对所有行(即所有病例)所对应的概率取均值(先基于总行数na求和再除以na)。鉴于此,AUC可理解为病例检测值比非病例检测值更大的平均概率,等价于“随机选择的病例比非病例更有可能被诊断为病例的概率”。公式(2)方括号内的部分还可以理解为,某个1右侧0的个数占0的总个数的比例,当以这个1对应的检测值为截断值时,其右侧的0将被正确地判断为阴性,故该比例即为真阴性率;方括号外部分可理解为以所有病例检测值作为截断值时的平均真阴性率,即AUC可理解为某检测指标用于疾病诊断时的平均真阴性率,即平均特异度。同理,基于公式(3)AUC可以理解为以所有非病例检测值为截断值时的平均真阳性率,即AUC可理解为某检测指标用于疾病诊断时的平均灵敏度。表1示例数据第(7)列和第(8)列的均值均为0.74,与基于公式(1)~(3)计算的AUC相同。
AUC含义也可通过图2所示的一维次序与二维非标化ROC曲线对应关系予以阐释。假定某检测指标将病例和非病例排序如下:1,1,1,……,1,0,0,0,……,0,即na个1均在前面,nn个0均在后面(此为最理想情况),此时对应的1的秩次总和为na×(na+1)/2,对应的非标化ROC曲线下格子数为na×nn。若因检测指标取值改变使得最后一个1与第一个0次序互换,则非标化ROC曲线在该位置的轨迹由原来的先竖线后横线变为先横线后竖线,曲线下格子数相应地减少1,但同时病例秩次总和(即1的秩次总和)增加1,1的秩次总和与曲线下格子数两者之和不变。任何一种1和0的排序均可视为在“na个1均在前面,nn个0均在后面”的基础上经若干次0和1次序互换的结果,且在次序互换的过程中,1的秩次总和与曲线下格子数两者之和始终保持恒定。当某一病例与某一非病例检测值相同时,1的秩次总和变化幅度为0.5,非标化ROC曲线下格子数也相应变化半个格子,和依然为定值。综上,1的秩次总和(记为∑Rank(1))与非标化ROC曲线下格子数(记为Sn)之和始终为na×nn+na×(na+1)/2,非标化ROC曲线下格子数Sn=na×nn+na×(na+1)/2-∑Rank(1),将其除以总格子数na×nn去量纲后即得另一AUC计算公式(4)。
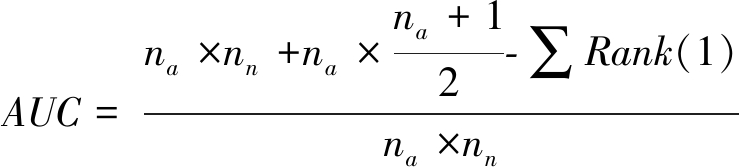
(4)
基于表1示例数据第(9)列计算的∑Rank(1)=81,在此基础上根据公式(4)计算的AUC为0.74,与根据公式(1)~(3)计算的AUC一致。通过公式(4)易知,当na和nn固定时,AUC大小主要取决于1的排序,某指标诊断性能越优,则1的次序越靠前,∑Rank(1)越小,对应的AUC越大,即AUC在本质上刻画了诊断指标对病例与非病例的区分性排序能力。
四、局限与思考
以上所有论证均假定病例检测值高于非病例检测值,但论证思路同样适用于病例检测值低于非病例检测值的情况;以上所有论证均假定检测值为连续变量,对于等级变量,将其量化赋值后同样可按上述思路进行分析。非标化ROC曲线能直观反映样本量,其曲线下面积的取值范围因样本量不同而不同。非标化ROC曲线有助于理解ROC曲线的含义及AUC的计算公式,但当样本量过大时,绘制非标化ROC曲线的现实意义有限。ROC曲线不能直观反映样本量,AUC取值范围介于0~1之间。
如前文所述,ROC曲线英文名称中的receiver的原意在很多情境中已不再适用。鉴于此,国外曾有学者[24]建议将ROC曲线更名为灵敏度—特异度曲线(sensitivity-specificity curve,S-S curve),但未得以推广,可能与ROC这一缩写已广为应用有关。也有学者建议将ROC理解成为relative operating characteristic curve[25],笔者对此很是认同,主要考虑如下:(1)relative与receiver首字母相同,ROC缩写可维持不变;(2)医学科研常用效应指标relative risk首个单词即为relative,其含义是“与…相比”;relative在relative operating characteristic curve中可解读为“与金标准相比”,某一检测指标用于疾病诊断时的相对性能,相应的AUC便可理解为实际的AUC与最理想状况(即取值为1.0)的比值。
综上,ROC曲线在本质上刻画了某定量指标对经金标准判定的二分类指标的排序轨迹,而AUC用于刻画该定量指标对该二分类指标做出正确归类的相对准确程度,它同时刻画出了平均真阳性率和平均真阴性率,且两者在数值上是相等的。
1 詹思延.流行病学.第八版.北京:人民卫生出版社,2017:131.
2 李立明.临床流行病学.北京:人民卫生出版社,2011:87-89.
3 Endrenyi L.Encyclopedia of biostatistics.Hoboken:John Wiley &Sons,Ltd,2005:4902.
4 Weld A.Statistical decision function.J Roy Stat Soc Ser A (Stat Soc),1950,46:165-205.
5 Peterson W,Birdsall T,Fox W.The theory of signal detectability.Trans IRE Professional Group Inf.Theory,1954,4:171-212.
6 Hanley JA.Receiver operating characteristic (ROC) methodology:the state of the art.Crit Rev Diagn Imaging,1989,29:307-335.
7 Lusted LB.Logical analysis in roentgen diagnosis.Radiology,1960,74:178-193.
8 Lusted LB.Decision-making studies in patient management.New Engl J Med,1971,284:416.
9 Lusted LB.General problems in medical decision making with comments on ROC analysis.Semin Nucl Med,1978,8:299-306.
10 Swets JA,Pickett RM.Evaluation of diagnostic systems.New York:Elsevier Inc,1982:46-67.
11 Metz CE.Basic principles of ROC analysis.Semin Nucl Med,1978,8:283-298.
12 宇传华.Roc分析方法及其在医学研究中的应用.第四军医大学,2000.
13 孙军,陈峰,郑凯尔.ROC曲线分析在放射学中的应用.中华放射学杂志,2001,35:574-577.
14 孙长亮.基于roc曲线的atr算法性能评估方法研究.国防科学技术大学,2006.
15 张晓龙,江川,骆名剑.ROC分析技术在机器学习中的应用.计算机工程与应用,2007,43:243-248.
16 李悦.非参数法与参数法估计roc曲线下面积的应用研究.广西医科大学,2007.
17 宋花玲,贺佳,黄品贤,等.ROC曲线下面积估计的参数法与非参数法的应用研究.第二军医大学学报,2006,27:726-728.
18 Eng J.Teaching receiver operating characteristic analysis:an interactive laboratory exercise.Acad Radiol,2012,19:1452-1456.
19 Zweig MH,Campbell G.Receiver-operating characteristic (ROC) plots:a fundamental evaluation tool in clinical medicine.Clin Chem,1993,39:561-577.
20 冯广龙,姜慧杰.ROC曲线分析在医学影像学诊断中的价值.中华医学杂志,2015,95:231-233.
21 Bamber D.The area above the ordinal dominance graph and the area below the receiver operating characteristic graph.J Math Psychol,1975,12:387-415.
22 Hanley JA,McNeil BJ.The meaning and use of the area under a receiver operating characteristic (ROC) curve.Radiology,1982,143:29-36.
23 Altman DG,Bland JM.Statistics notes:Diagnostic tests 3:Receiver operating characteristic plots.Br Med J,1994,309:188-188.
24 Brismar J.Understanding receiver-operating-characteristic curves:a graphic approach.AJR Am J Roentgenol,1991,157:1119-1121.
25 Swets JA.Measuring the accuracy of diagnostic systems.Science,1988,240:1285-1293.